Blogsheet week 10
In this week’s lab, you will collect more data on low pass
and high pass filters and “process” them using MATLAB.
PART A: MATLAB
practice.
Open MATLAB. Open the editor and copy paste the following code. Name your code as FirstCode.m
Open MATLAB. Open the editor and copy paste the following code. Name your code as FirstCode.m
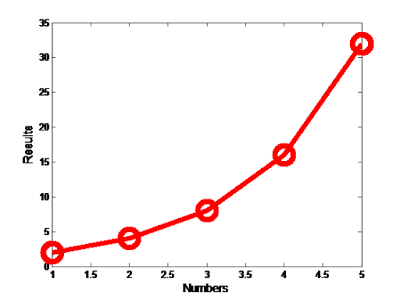
Save the resulting plot as a JPEG image and
put it here.
clear all;
close all;
x = [1 2 3 4 5];
y = 2.^x;
plot(x, y, 'LineWidth', 6)
xlabel('Numbers', 'FontSize', 12)
ylabel('Results', 'FontSize', 12)
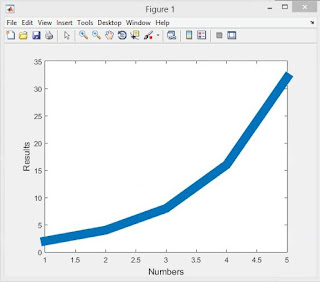 |
| This is an image of the plot we got with the above MATLAB code |
What does clear
all do?
Clear all clears all data and objects from the work space and closes the MuPAD engine which resets all of the programs assumptions.
What does close
all do?
The close all function deletes all figured whose handles are not hidden.
In the command line, type x and press enter. This is a matrix. How many rows and columns are
there in the matrix?
1 row 5 columns.
Why is there a semicolon at the end of the line
of x and y?
When you are defining component equations you have to end the functions with a semicolon otherwise it will result in an error. MATLAB needs the semicolon so it knows that is a function or definition, if you do not do this it results in an error message displaying an "unexpected MATLAB expression".
Remove the dot on the y = 2.^x; line and execute
the code again. What does the error message mean?
The error message means that we are giving x values in vector quantities and our y is trying to display scalar quantities so if we put the dot before the exponent it will result in a vector output.
How does the LineWidth affect the plot? Explain.
The LineWidth 1 is equal to having a simple plot of x and y. If you keep increasing the line width it increases the thickness of the line, possibly to make it easier to differentiate from others in the same plot.
Type help
plot on the command line and study the options for plot command. Provide how you would change the line for plot command to obtain the following
figure (Hint: Like ‘LineWidth’, there
is another property called ‘MarkerSize’)
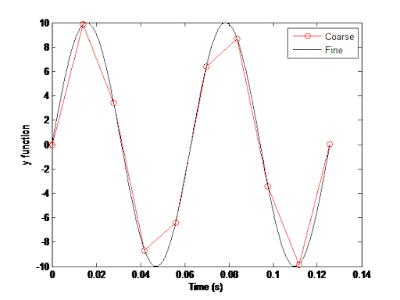
 |
| Fig. 1 |
You would alter the line for the plot to "plot(x, y, '-ro', 'LineWidth', 4, 'MarkerSize', 16)"
What happens if you change the line for x to x
= [1; 2; 3; 4; 5]; ? Explain.
From what we can tell nothing changes in the plot that the code executes. Basically the semi-colon defines all the numbers in the brackets to x. When you add a semi-colon behind each number it is doing the same thing, but in a different way.
Degree vs. radian in MATLAB:
a.
Calculate sinus of 30 degrees using a calculator
or internet.
sin(30) = .5
sin(30) = .5
b.
Type sin(30) in the command line of the MATLAB. Why
is this number different? (Hint: MATLAB treats angles as radians).
This number is different because when you use a calculator or the internet it generally calculates sin as a degree, while MATLAB gives answers as rads.
c.
How can you modify sin(30) so we get the correct
number?
sin(30*2*pi/360)
2 Plot y =
10 sin (100 t) using Matlab with two different resolutions on the same plot: 10 points per period and
1000 points per period. The plot needs to show only two periods. Commands you might need to use are linspace, plot,
hold on, legend, xlabel, and ylabel. Provide your code and resulting figure.
The output figure should look like the following:
 |
| Fig 2. |
clear all;
close all;
t1 = linspace(0, (4*pi)/100, 10);
t2 = linspace(0, (4*pi)/100, 1000);
y1 = 10*sin(100*t1);
y2 = 10*sin(100*t2);
plot(t1, y1, '-ro', t2, y2)
xlabel('Time (s)')
ylabel('y function')
legend('course', 'fine')
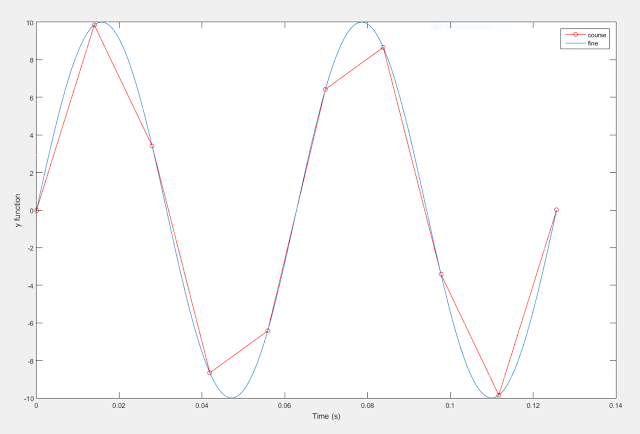 |
| Our graph generated by the code above |
Explain what is changed in the following plot
comparing to the previous one.
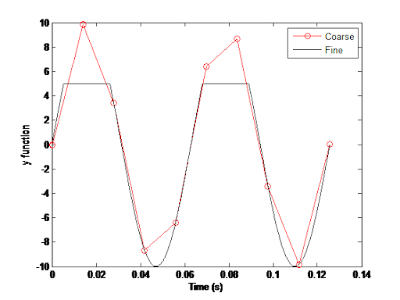 |
| Fig. 3 |
In the graph in figure 3, the coarse line remains the same as in fig. 2 and the fine line differs from fig.2 because it is clipping the top of the sinusoidal line.
The command find
was used to create this code. Study the use of find (help find) and try to replicate the plot above. Provide your code.
PART B: Filters and
MATLAB
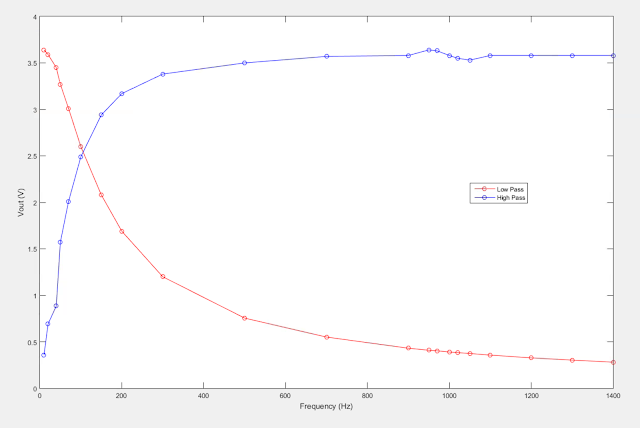
Plot your data using MATLAB. Make sure to use
proper labels for the plot and make your plot line and fonts readable. Provide
your code and the plot.
clear all;
close all;
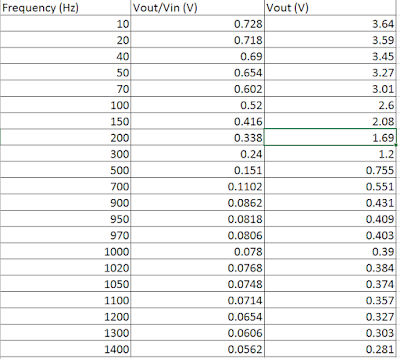
Frequency = [10 20 40 50 70 100 150 200 300 500 700 900 950 970 1000 1020 1050 1100 1200 1300 1400];
LPvoltage = [3.64 3.59 3.45 3.27 3.01 2.6 2.08 1.69 1.2 0.755 0.551 0.431 0.409 0.403 0.39 0.384 0.374 0.357 0.327 0.303 0.281]
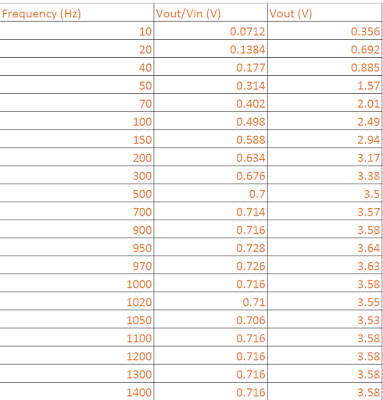
HPvoltage = [0.356 0.692 0.885 1.57 2.01 2.49 2.94 3.17 3.38 3.5 3.57 3.58 3.64 3.63 3.58 3.55 3.53 3.58 3.58 3.58 3.58]
plot (Frequency, LPvoltage, 'o-r')
hold on;
plot (Frequency, HPvoltage, 'o-b')
hold on;
xlabel('Frequency (Hz)')
ylabel('Vout (V)')
Calculate the cut off frequency using MATLAB. find command will be used. Provide your
code.
clear all;
close all;
Frequency = [10 20 40 50 70 100 150 200 300 500 700 900 950 970 1000 1020 1050 1100 1200 1300 1400];
LPvoltage = [3.64 3.59 3.45 3.27 3.01 2.6 2.08 1.69 1.2 0.755 0.551 0.431 0.409 0.403 0.39 0.384 0.374 0.357 0.327 0.303 0.281]
plot (Frequency, LPvoltage, 'o-r')
hold on;
xlabel('Frequency (Hz)')
ylabel('Vout (V)')
legend('Low Pass')
y = find(LPvoltage<(.707*5));
for n=1: length(y)
m(n)= y(n)
a(n)= Frequency(m(n))
end
fcLP = max(a(n))
plot([fcLP,fcLP], [0,4], '--r');
for n=1: length(y)
m(n)= y(n)
a(n)= Frequency(m(n))
end
fcLP = max(a(n))
plot([fcLP,fcLP], [0,4], '--r');
clear all;
close all;
Frequency = [10 20 40 50 70 100 150 200 300 500 700 900 950 970 1000 1020 1050 1100 1200 1300 1400];
HPvoltage = [0.356 0.692 0.885 1.57 2.01 2.49 2.94 3.17 3.38 3.5 3.57 3.58 3.64 3.63 3.58 3.55 3.53 3.58 3.58 3.58 3.58]
plot (Frequency, HPvoltage, 'o-b')
hold on;
xlabel('Frequency (Hz)')
ylabel('Vout (V)')
legend('High Pass')
x = find(HPvoltage<(.707*5));
for n=1: length(x)
m(n)= x(n)
z(n)= Frequency(m(n))
end
fcHP = max(z(n))
plot([fcHP,fcHP], [0,4], '--b');
close all;
Frequency = [10 20 40 50 70 100 150 200 300 500 700 900 950 970 1000 1020 1050 1100 1200 1300 1400];
HPvoltage = [0.356 0.692 0.885 1.57 2.01 2.49 2.94 3.17 3.38 3.5 3.57 3.58 3.64 3.63 3.58 3.55 3.53 3.58 3.58 3.58 3.58]
plot (Frequency, HPvoltage, 'o-b')
hold on;
xlabel('Frequency (Hz)')
ylabel('Vout (V)')
legend('High Pass')
x = find(HPvoltage<(.707*5));
for n=1: length(x)
m(n)= x(n)
z(n)= Frequency(m(n))
end
fcHP = max(z(n))
plot([fcHP,fcHP], [0,4], '--b');